题目 Title

An Exact Solution to the Linearized Richards Equation for Layered Media With Flexible Initial Condition.

期刊 Journal

Water Resources Research (IF=5.4)

作者 Author

Chen ZL; Huang YY; Fang HW; Yeh TCJ; Zha YY

摘要 Abstract

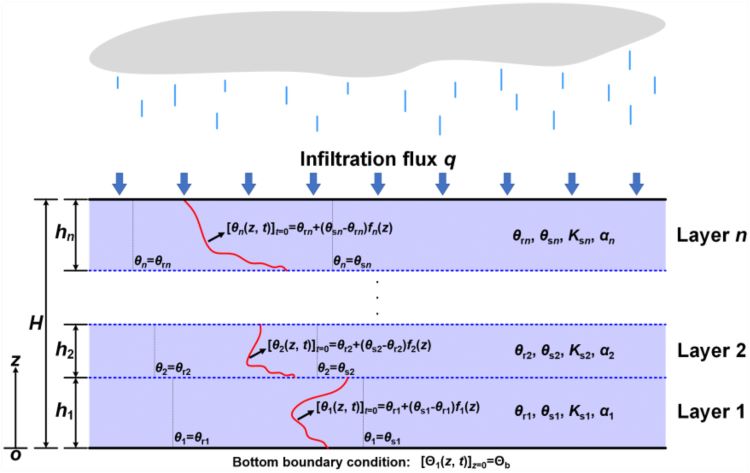
Srivastava and Yeh (1991, https://doi.org/10.1029/90WR02772) derived an exact solution to the linearized Richards equation (LRE) for two-layer medium infiltration using the Laplace transform (LT) method with a particular initial condition assumed, making the most pioneering contribution to the derivation of exact solutions to the layered-medium LRE (i.e., ES-LMLREs). However, the LT method is unsuitable for deriving an ES-LMLRE that considers either an arbitrary initial condition or an arbitrary number of layers, or both, preventing further progress in developing ES-LMLREs. Adopting a new solution strategy, namely a conjunctive use of the variable separation method and the transfer matrix method, we develop a novel exact layered-medium-LRE infiltration solution, overcoming the above difficulties. First, the proposed solution is successfully validated against the Srivastava-Yeh solution. As a feature-demonstration example, a layered-medium water absorption process is simulated, and our solution well captures how the heterogeneity of hydraulic parameters affects the dynamics of this process. Moreover, the proposed solution is a valuable benchmark for related numerical models.

简介 Brief introduction

Srivastava和Yeh（1991，https://doi.org/10.1029/90WR02772）使用拉普拉斯变换（LT）方法，在假设特定初始条件的情况下，推导出了两层介质入渗问题的线性化Richards方程（LRE）精确解，为分层介质LRE精确解（即ES-LMLREs）的推导做出了最具开拓性的贡献。然而，LT方法不适合用来求解考虑任意初始条件或任意层数介质，或同时考虑以上两者情况下的ES-LMLRE，这阻碍了 ES-LMLREs 的进一步发展。我们通过采用一种新的求解策略，即联合使用分离变量法和传递矩阵法，克服了上述困难，开发了一种新的ES-LMLRE。首先，通过与Srivastava-Yeh解进行对比，成功验证了本文解的正确性。其次，作为一个代表性示例，模拟了分层介质的吸水过程，本文解很好地捕捉了水力参数的异质性如何影响这一动态过程。此外，本文提出的精确解可以作为相关数值模型的基准解。

扫码关注立方体公众号，实时追踪课题组最新科研进展